量子版ムーアの法則

古典コンピュータの世界では、フェアチェイルドとインテルの共同創立者ゴードン・ムーアが１９６５年に提唱したムーアの法則（経験則）がありますが、これが量子コンピュータにも適用できるかもしれないと議論されています。

※参考記事

ムーアの法則

これは半導体ウエハ上に形成されるトランジスタ部品の数が年に２倍になるという予測でしたが、これは後日２年で２倍と修正されました。

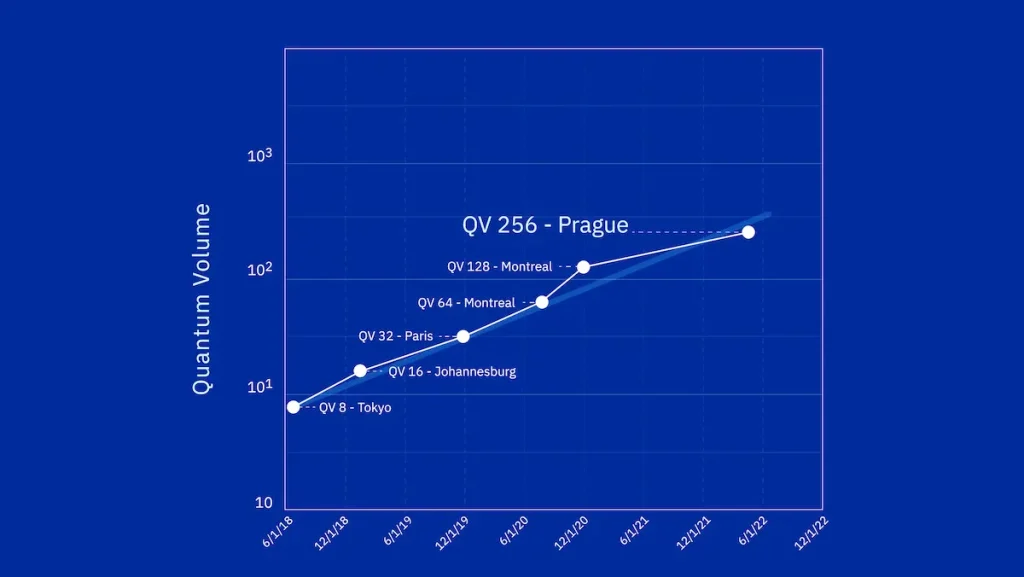
量子版ムーアの法則は、いまのところ、１年で２倍の速度で進行しています。

IBMは、falcon r10 で256QVを達成したと発表しました。

Quantum Volume は量子コンピューターの性能尺度で、論理量子ビット数の２乗に比例する指標ということです。

上記IBMの報告によれば、QV256は、2qubitで99.9％のゲート忠実度を持つということです。つまり、1,000回に1回しかエラーが発生しない性能です。2qubit論理ゲートを8ステップ動作させて8qubit試験を実施した時、95パーセントの信頼度で平均68.5％の時間で正しい計算ができたということです。これは2論理qubitが完成したとは言えないですけど、8論理qubitが大体使えるようになったとも言える状況でしょうか。

さて、ビットコインの暗号強度を量子ビット数に換算すると、

https://arxiv.org/pdf/1706.06752.pdf

こちらの論文では、ビットコイン同等の暗号強度を突破するのに2330論理qubitの量子コンピューターが必要とされると見積もりされています。

さて、2022年の256QVを仮に2論理qubit相当と無理矢理仮定して、1年で2倍のQV性能向上があるとしますと、2330論理qubitに到達するまで何年かかるでしょうか。QVが論理ビットの２乗の尺度なので、QVが２倍になるということは、√2倍の論理ビットの性能向上ということになります。

$$2330=2 \times \sqrt{2}^n, 1165 = \sqrt{2}^n$$

としますと、

$$n = \log_\sqrt{2}1165 = 20.37$$

ということで、21年後には2330論理qubit付近が実現できるかもしれないということになります。それは（ビットコインの暗号が破られちゃうかもしれないのは）、えーと、2022+21＝2043年ということになるのですが、本当でしょうか！！2043年って、カーツワイルさんが予言しているシンギュラリティの2045年に近い数値で驚いてしまいます！！

まあ、NISTの耐量子暗号策定プロジェクトも佳境に入ってきておりますので心配は要らないのですが、bitcoin core など暗号資産のプログラムは21年以内に耐量子アドレスを追加しなければならないのではないかと予想されていることになります。

※参考記事

耐量子暗号