ビットコインなどの暗号通貨を利用する人は常に暗号強度に注意を払う必要があります。古今東西破られなかった暗号は無いからです。
post quantum cryptography 耐量子暗号プロジェクト、略してPQC、アメリカ国立標準技術研究所NISTで進行中のプロジェクトです。量子コンピューターが実用化されても破られない暗号の標準化を企図するプロジェクトです。
satoshi nakamoto は紛れもなく天才でしたし、256ビットの楕円曲線暗号は、スパコンも含めた従来型の古典コンピューターの従来の性能向上を考慮に入れても十分に安全な暗号であると考えられてきました。
https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-57pt1r5.pdf
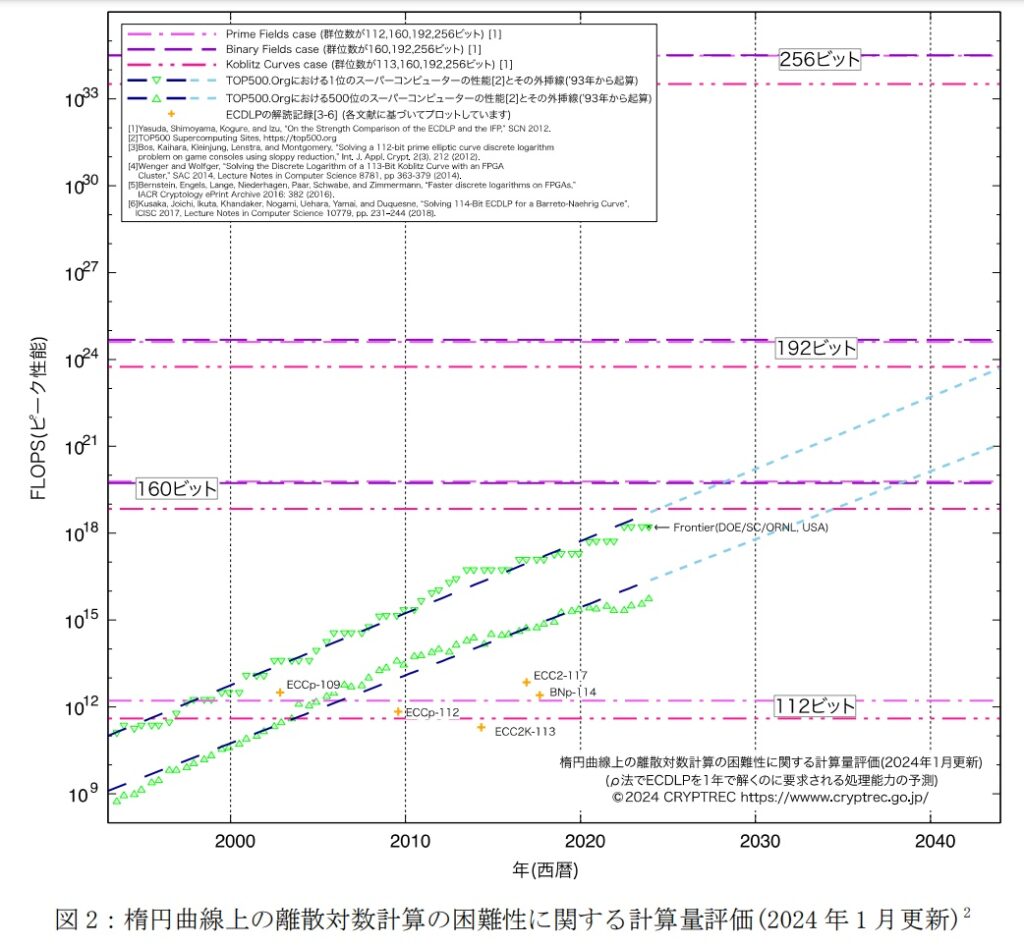
256bitの楕円曲線暗号の強度は、3072bitのRSA暗号に匹敵するとされ、これを1年間で解読するには10の33乗FLOPSの計算量が必要とされ、2024年現在の世界最高のスーパーコンピューターFrontierが10の18乗FLOPSの能力なので、10の15乗年間の総当たり計算が必要な暗号強度です。10の15乗年間とは、10の8乗で1億年、10の12乗で1兆年ですから、1000兆年ということになります。しかしこの、frontier の消費電力は22703KWと言いますから物凄い計算パワーです!
グラフではtop500.org における1位のスーパーコンピューターの性能進化の状況が点線で予想されているのですが、独断と偏見により、この性能進化が256bit楕円曲線暗号のレベルに到達する時期は、10年で300倍、20年で10万倍(10の5乗)と読み取れますので、60年後ということになります。60年後(2084年頃)に世界最高のスーパーコンピューターを使って1年間計算すれば、256ビット楕円曲線暗号が解読できるかもしれないということです。
CRQC(Cryptographically Relevant Quantum Computer)
暗号解読可能量子コンピューターの時代がすぐそこまで来ています。
https://www.cryptrec.go.jp/report/cryptrec-rp-2000-2023.pdf
2009年当時、これほど量子コンピューターの開発が急速に進展するとは予想できませんでした。satoshi nakamoto は暗号学の専門家でしたが、量子コンピューターの専門家では無かったのです。古典コンピューターの進歩に関するムーアの法則は考慮に入れていましたが、量子コンピューターの進歩に関する量子版ムーアの法則は考慮に入れていませんでした。
1994年に提案されたショアのアルゴリズム(量子コンピューターが離散フーリエ変換を高速に計算できることにより素因数分解の計算速度を指数関数的に向上できるとするもの)は知られていましたが、量子コンピューターによる量子超越性の実現がこれほどの速度で進展するとは想像できなかったのです。
量子コンピューターが離散フーリエ変換を高速に計算できるというのは、電子の動きがフーリエ変換そのものであり、量子力学のシュレーディンガー方程式にフーリエ変換が含まれているということを意味するのでしょう(注=管理人の理解)。だから量子、例えば電子のエネルギー準位を観測することは、フーリエ変換を計算することと同値になるのです。計算したければ観測すれば良いのです。ここを突破口にして、従来型の離散対数問題(y=x^mとしたときにyからmを求めること)を用いた全ての暗号が危険に晒される可能性があることが判明したのです。
ですから、量子コンピューターの時代を生きる我々は常に、量子コンピューターの開発状況と、耐量子暗号技術の開発状況をウォッチし続ける必要があります。
量子耐性台帳(P2QRH,P2QS)
今後おそらく、ビットコインのハードフォーク(アップデート)で、耐量子暗号で署名できる新しいアドレス(P2QRH pay to quantum resistant hash, P2QS pay to quantum secure)が追加されることになるでしょう。量子耐性台帳Quantum Resistant Ledger の導入です。 その日が来たら、我々は新しいアドレスに移行する必要があります。送金時に複数の署名を要求するマルチシグアドレスはビットコインの暗号強度を高める試みの一つとも言えますが、根本的に強度を上げる仕組みではありません。例えば100個の署名を要するマルチシグアドレスの暗号強度は通常アドレスの100倍になります。ビットコイン残高を100分割して100個のアドレスに分散保存しても良いでしょう。
ビットコインを安全に使い続けるためには量子力学の勉強が不可欠です。
そうは言っても、管理人も含めた一般人には限界があります。そこで、楕円曲線暗号の暗号強度の見積りと、量子コンピューターの開発状況をウォッチすると良いでしょう。偉い人たちが毎日論文を書いて査読してくれているのですから、それを読めば良いのです。
楕円曲線暗号の暗号強度見積もり
https://arxiv.org/pdf/1706.06752.pdf ビットコイン同等の暗号強度を突破するのに2330論理qubitの量子コンピューターが必要とされる。
https://arxiv.org/pdf/1902.02332v2.pdf これはエラー訂正を考慮すると6770万物理qubitに相当します。
https://cacm.acm.org/magazines/2013/10/168172-a-blueprint-for-building-a-quantum-computer/fulltext ビットコイン相当の2048ビット素因数分解に必要な規模は60億物理QBITと見積もった論文。
https://arxiv.org/pdf/1010.5022.pdf Nbit素因数分解には6倍の論理QBITが必要であること、エラー訂正のために論理QBITの6240倍の仮想QBITが必要であることを報告した論文。つまり2048bit素因数分解なら、7667万仮想QBITが必要。
https://arxiv.org/pdf/1905.09749.pdf 2048bit素因数分解には2千万物理QBITで足りるとする論文。
https://arxiv.org/pdf/2505.15917 2048bit素因数分解には100万物理QBITで足りるとする論文。
量子コンピューターの開発状況
2024年8月現在 IBM eagle 127論理qubits(NISQ)
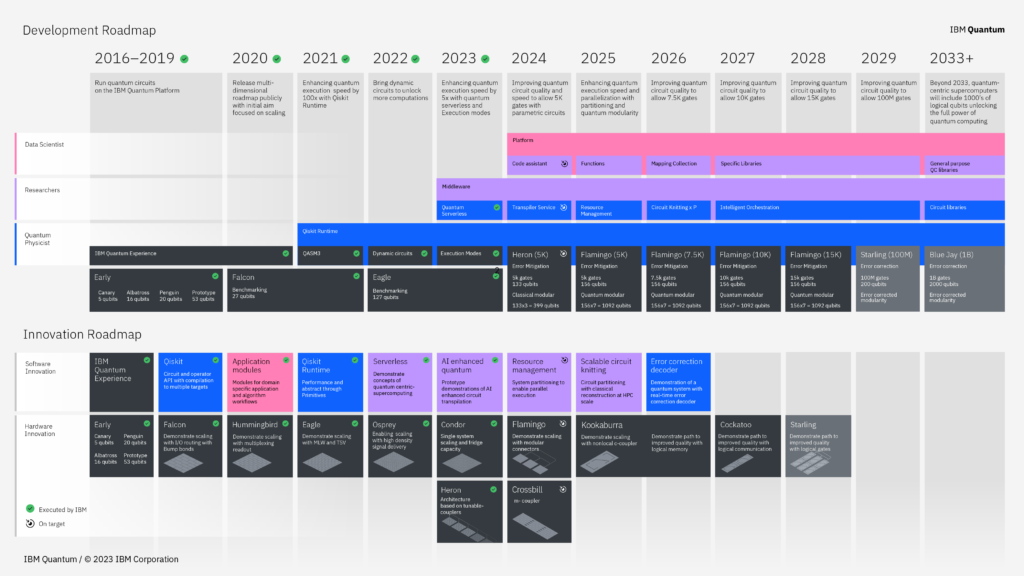
こちらのロードマップの2024年の項目を引用します。
Error Mitigation 5k gates 133 qubits
Classical modular 133×3=399 qubits
5000 物理量子ビットで133論理量子ビットを目指す
エラー緩和型量子コンピューターということです。
そして古典モジュールと題して、133を3倍して399量子ビットと記載しているのですが、これは量子コンピューターのことを何も知らない人を騙そうとする記載です。133ビットの量子コンピューターが3台あっても399量子ビットの量子コンピューターとは全然違うものです。
楽天からの出資も受け入れているQuEra Computing Inc.が256qbit デバイスの構築を完了したと発表。
google では2029年にエラー耐性量子コンピューターを商業実用化させると主張しています。
日本のCRYPTREC(Cryptography Research and Evaluation Committees,暗号研究および評価委員会)の2020年報告書には次のような文言があります。
量子コンピュータにおける素因数分解・離散対数問題について
量子コンピュータにおいてShorのアルゴリズムによる素因数分解を試みた結果として、適切に素因数分解されたと言える最大の数は21(=3×7)であり、35(=5×7)の素因数分解には失敗している。
2020年12月に、世界初となる量子コンピュータにおける離散対数問題の求解実験の成功について、
当事者であるNICTより報告があり、2^z≡1 mod 3 については良い出力を得られているものの、2^z≡2 mod 3 については失敗している。
いずれも現在の量子コンピュータで、暗号で用いられるような大きなパラメータの問題が解けるとは考えにくい状況。
つまり理論上の懸念と、実際上の懸念は別ということのようです。現在の量子コンピューターはNISQと呼ばれており誤り訂正が不完全な一種のアナログコンピューターですが、100万qubit以上になるとエラー訂正ができるFault-tolerant quantum computer(FTQC)になると言われており、このNISQ時代が最低でも2030年までは続くと言われています。NISQでは公開鍵暗号を解くことはできません、FTQC時代が来るまで、少なくとも2020年代は心配無用です。FTQC時代になっても2330論理qubitが必要ですから直ちに危険という訳でもありません。量子版ムーアの法則で試算すると、2043年頃に量子コンピュータを使ってビットコインの暗号が破られる可能性があるようです。
Y2Q時計
非営利団体Cloud Sequrity Alliance は量子コンピューターがRSAなど既存の暗号を破る可能性がある時期として2030年4月14日を設定し、この日までのカウントダウン時間を表示するY2Q時計を公開しています。この期日に本当に量子コンピューターが既存暗号を破るかどうかは不明ですが、とにかくそのように推測している専門家も居るということです。CSAはクラウドセキュリティの業界団体ですので「セキュリティ対策にお金を使ってください」というポジショントークの可能性も勿論あると思いますが、2000年問題のY2Kに似せた警告方法です。
我々は量子力学と暗号技術を勉強し、量子コンピューターを「正しく恐れる」必要があります。これからしばらく、量子コンピュータのニュースでビットコインが暴落した時は「全力買い」で宜しいかと思われます。
※2024/8/18追記
アメリカ国立標準技術研究所NISTが、とうとう耐量子公開鍵暗号の標準化文書の初版を発行しました。
※標準化文書はこちら
https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.203.pdf
それはML-KEM(CRYSTALS-KYBERの発展形)という格子暗号(多元連立方程式問題)ですが、LWE問題というノイズを加えた多元連立方程式となっているため、量子フーリエ変換を使っても簡単には計算できない仕組みです。ノイズを加えるのは、連立方程式をガウスの消去法で解けないようにするためです。できる限り「総当たり方式(ブルートフォース攻撃)」じゃないと解けない数学問題が必要なのです。
※参考記事、システム制御情報学会65巻2号より「量子コンピュータに耐性のある暗号技術と標準化の動向」
https://www.jstage.jst.go.jp/article/isciesci/65/2/65_60/_pdf
こちらの記事によるとCRYSTALS-KYBERの秘密鍵の長さは1632バイトということで、ビットコインに使われているsecp256k1の秘密鍵は256bit(32バイト)なので桁違いですね!仮に従来通りの楕円曲線暗号を用いたとしても秘密鍵が1632バイトなら暗号強度が桁違いの強さになります。32→1632ですから 2桁違いますね!
標準化されたML-KEMの秘密鍵の長さは、ML-KEM-512、ML-KEM-768、ML-KEM-1024の3種類が設定されており、最長で1024ビット(128バイト)となりました。
※2024/2/17追記
米AWS(Amazon)、米Google、米NVIDIA、米Cisco、米IBMをプレミアメンバーとするPost-Quantum Cryptography Alliance(耐量子暗号組合)がLinux Foundation傘下に設立されました。
MIT ライセンスのオープンソースソフトウェアもgithubリポジトリで公開されています。耐量子暗号を使ったhttps通信を実現できるOpenSSL3の改良版 oqs-providerと、耐量子アルゴリズムのライブラリ liboqs です。耐量子暗号の社会実装が一気に加速することが期待されます。勿論、暗号資産の新しいアドレス形式にも使われるでしょう。耐量子アドレスの導入も時間の問題です。
※2024/2/26追記
アップルがios17.4から耐量子暗号PQ3をiMessageに導入すると発表しました。これは、将来の量子コンピューター実用化後に、過去の通信記録の暗号を無効化されないようにする予防措置です。capture now, decrypt later 攻撃の予防です。
この対策はopen SSH9.0でも導入されています。
SSH9.0リリースノートより
ssh(1), sshd(8): use the hybrid Streamlined NTRU Prime + x25519 key exchange method by default (“sntrup761x25519-sha512@openssh.com”).
The NTRU algorithm is believed to resist attacks enabled by future quantum computers and is paired with the X25519 ECDH key exchange (the previous default) as a backstop against any weaknesses in NTRU Prime that may be discovered in the future. The combination ensures that the hybrid exchange offers at least as good security as the status quo.
We are making this change now (i.e. ahead of cryptographically-
relevant quantum computers) to prevent “capture now, decrypt
later” attacks where an adversary who can record and store SSH
session ciphertext would be able to decrypt it once a sufficiently
advanced quantum computer is available.
SSHセッションの暗号文を事前に保存した敵対者が、後日、十分に高度な量子コンピュータが利用できるようになると、その暗号文を復号化できるようになってしまうという” capture now, decrypt later” 攻撃を防ぐために、今(つまり暗号学的に意味のある量子コンピュータ実用化に先駆けて)行っているのです。
暗号資産時価総額・・・260兆円
世界マネーサプライ・・・40160兆円(0.65%到達)
金の時価総額・・・1330兆円(19.5%到達)
金の半分まで暗号資産が買われると仮定したBTC目標価格・・・1433万円
※参考記事
※参考書籍




コメントを残す