楕円曲線暗号はドーナツの表面に描かれていることを知った話

光成滋生、暗号と認証のしくみと理論がしっかりわかる教科書

盛り沢山で難しい教科書ですが、一点だけ、この本で知ったことがありました。スモールステップで学びを進めることができました。それはビットコインに使われている公開鍵暗号の楕円曲線暗号です。secp256k1のカタチです。

https://en.bitcoin.it/wiki/Secp256k1

ビットコインの仕組みは複雑なものですが、最も根本的な仕組みは、Secp256k1 と呼ばれる関数の知識です。それは、$$y^{2}=x^{3}+7 \pmod{2^{256} – 2^{32} – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1}$$

この右側のmodの部分ですね。256ビットの巨大な素数ｐ（10進数で78桁！）で割り算した余りの世界、ゼロからｐ－１までの世界にある楕円曲線というわけです。このようにx軸もy軸も特定の数で割り算した余りですよ、と宣言しますと、xy平面が無限に広がっていくことにはならず、ｐ未満の整数の世界に限定されるわけです。１ずつ足していくと、時計の針みたいに数字が増えて行ってまたゼロに戻るということです。そういうものを「有限体・ガロア体」と言います。ビットコインの楕円曲線は、整数の有限体上に描かれた楕円曲線なのですね。10進数で78桁という巨大な有限体ですが、頭と尻尾が繋がっているレッキとした有限体なのです。時計の針のようにグルグル回っているわけです。

四則演算が成立するような有限集合はエヴァリスト・ガロアが発見したので、ガロア体と呼ばれています。ガロアというのは２０歳で決闘で亡くなったというのですが、「数とは何か」ということについての新しい定義（それは「群」というものですが）を与えた人であり、数の概念を拡張した人なので、驚くしかない天才です。

鈴木智秀、図解と実例と論理で、今度こそわかるガロア理論

いまここに、正方形のゴム板（ゴムシート）があるとして、上下をくっつけまして、トイレットペーパーの芯みたいな円筒を作成し、横に置いた円筒の左右をくっつけますと、これはドーナッツ（トーラス）の形になるのです。

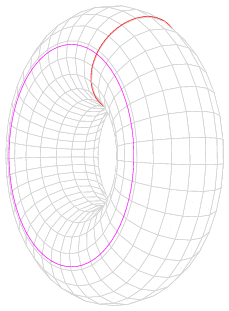
従って、ビットコインの楕円曲線はトーラスの表面上に描かれて、その表面上の座標空間においてスカラー倍算を繰り返すことによって、秘密鍵から公開鍵を計算することができるのです。ビットコインの暗号はドーナツを使って計算されているということです。

※参考記事

楕円曲線暗号の一方向性